Spring Constant Unit and Dimension

WHAT IS SPRING CONSTANT ?

Spring constant(k) is the constant of proportionality or the amount of energy delivered proportionality in the Hooke’s law experimental trial.

Stronger or stiffer springs will have higher spring constant. For a specific mass added to the spring, springs with higher the spring constant will have more modest(smaller) displacement than that of the springs with lower spring constant value.

Spring constant is the angle of the straight-line part of the chart, force in newton versus extension in meter.

SIGNIFICANCE OF SPRING CONSTANT

Spring constant worth assumes a significant part in the plan and assembling of springs.

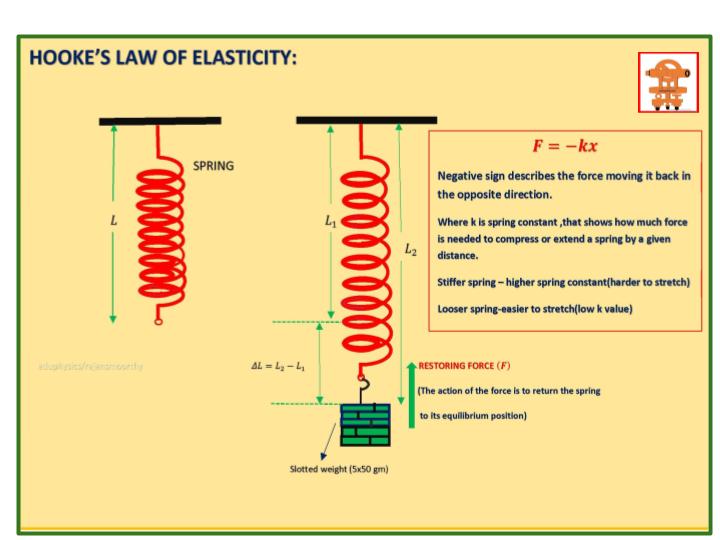
Hooke’s law of elasticity experiment (the straight connection between the expansion of a spring and the restoring force) is utilized to ascertain the spring constant and the necessary force for the particular applications like apparatuses hardware, toys, clinical instruments and so on.

Hooke’s law spring constant value is special (unique) to each spring that gives a thought regarding the firmness, aspect, state of the given spring expected to compress or expand a spring by a given distance within the elastic limit

SPRING CONSTANT FORMULA

 

Fun Fact: Sprial Spring

Did you know that springs aren’t just man-made? Nature has its own springs!For example

• The tendons in your legs act like springs when you run or jump,storing and releasing energy efficiently.
• DNA molecules behave like tiny springs stretching and coiling under forces at the molecular level.

How to measure the spring constant?

Want to find the spring constant of a spring? Here’s the simple experiment you can try.

• Hang a spring vertically and measure its natural length.
• Attach a known mass ‘m’ to the spring and measure the new length.
• Calculate the displacement x and use Hooke’s law k=mg/x where g is the acceleration due to gravity.

Real-world applications

Weighing scales

A spring with precise spring constant values can be used to measure the weight of an item. The spring constant specifies how much the spring will compress under a particular load.

Door closers

Springs are used in door closer to close the door automatically.The spring constant value controls how fast or slowly the door closes.

Trampolines

Trampolines employ springs to produce a bouncing surface.The spring constant of the trampoline’s spring influences how much the trampoline will bounce.

Shock-absorbers

Spring is used to cushion stress and vibration. The exact spring for a comfortable ride is determined by the spring constant.

Aerospace

To guarantee safety, springs with properly determined spring constants are used in aerospace engineering.

Sports equipment

The design of sports equipment, including tennis rackets and golf clubs relies on springs with specific spring constants to optimise the performance.

Medical devices

Springs are used in various medical devices like insulin pumps and other devices and are crucial for functionality and patient comfort.

UNIT OF SPRING CONSTANT

DIMENSIONAL FORMULA OF SPRING CONSTANT

Dimensions:The language of physics

To truly understand the spring constant, we must express it in terms of its fundamental dimensions.In the international System of units(SI), the dimensions of force are F=[MLT]^-2 where

• [M] represents mass
• [L] represents length
• [T] represents time

And the dimensions of displacement are 

• Displacement (x) : [L]

Therefore the dimensions of the spring constant are  k=F/x

     = [MLT]^-2 /L

     = [M] [T]^-2

Spring Constant Units in Different Measurement Systems

	System	Unit of force           F	Unit of displacement               x	Unit of Spring constant                 k
1.	SI units	newton (N)	meter (m)	N/m
2.	CGS units	dyne (dyn)	Centimeter                                    (cm)	dyn/cm
3.	Imperial units	Pound-force          (lbf)	Inch(in) or foot(ft)	lbf/in or lbf/ft

Dimension of spring constant

What  do these dimensions mean?

• Mass Dependency :[Mass] (mass) : The spring constant  depends on the  material properties of the spring such as its density and stiffness,A stiffer spring (higher k) generally requires a larger mass to produce the same displacement

• Time Dependency: [Time]^-2  (Time)^-2: This reflects the oscillatory nature of springs when  a mass is attached to a spring it oscillates with a frequency that depends on ‘k’.

Beyond the equation:

While the dimensional analysis provides a foundational understanding, the true significance of the spring constant lies in its practical applicationsFrom shock absorbers in vehicles to the delicate balance of a diving board,springs play a crucial role in our everyday lives.By understanding the dimensions and behavior of the spring constant, engineers and scientists can design and optimize systems that rely on these remarkable devices.

NUMERICAL ON SPRING CONSTANT

Numerical 1

Numerical 2

Numerical 3

Numerical 4

CONCLUSION

The spring are vital parts found in machines, motors apparatuses, carport entryways, mousetraps, vehicles, toys, clinical instruments, etc. The force of a spring which produces mechanical energy when delivered. Knowing the spring constant, exceptional worth of the specific spring assists us with choosing the right plan. Did you at any point ponder the justification behind at least two springs associated in series or parallel?